In Part 9 of the LFCA series, we covered the basics of IP addressing. To better understand IP addressing, we need to pay more attention to these two types of IP address representation – binary and decimal-dotted quad notation. As mentioned earlier, an IP address is a 32-bit binary number that is usually represented in decimal format for ease of readability.
The binary format uses only the digits 1 and 0. This is the format that your computer comprehends and through which data is sent across the network.
However, to make the address human-readable. It is conveyed in a dotted-decimal format which the computer later converts into binary format. As we stated earlier, an IP address is made up of 4 octets. Let’s dissect the IP address 192.168.1.5.
In the dotted-decimal format, 192 is the first octet, 168 is the second octet, 1 is the third, and lastly, 5 is the fourth octet.
In binary format the IP address is represented as shown:
11000000 => 1st Octet 10101000 => 2nd Octet 00000001 => 3rd Octet 00000101 => 4th Octet
In binary, a bit can be on or off. The ‘on‘ bit is represented by 1 while the off bit is represented by 0. In decimal format,
To arrive at the decimal number, a summation of all the binary digits to the power of 2 is carried out. The table below gives you the positional value of every bit in an octet. For example, the decimal value of 1 equates to the binary 00000001.

In better format, this can also be represented as shown.
2º = 1 = 00000001 2¹ = 2 = 00000010 2² = 4 = 00000100 2³ = 8 = 00001000 2⁴ = 16 = 00010000 2⁵ = 32 = 00100000 2⁶ = 64 = 01000000 2⁷ = 128 = 10000000
Let’s try to convert an IP address in dotted-decimal format to binary.
Converting Decimal Format to Binary
Let’s take our example of 192.168.1.5. To convert from decimal to binary, we will start from left to right. For every value in the table, we ask the question, can you subtract the value in the table from the decimal value in the IP address. If the answer is ‘YES‘ we write down ‘1‘. If the answer is ‘NO‘, we put a zero.
Let’s start with the first octet which is 192. Can you subtract 128 from 192? The answer is a big ‘YES‘. Therefore, we will write down 1 which corresponds to 128.

192-128 = 64
Can you subtract 64 from 64? The answer is ‘YES’. Again, we jot down 1 which corresponds to 64.

64-64 = 0 Since we have depleted the decimal value, we assign 0 to the remaining values.

So, the decimal value of 192 translates to the binary 11000000. If you add the values corresponding to 1s in the bottom table, you end up with 192. That is 128 + 64 = 192. Makes sense right?
Let’s proceed to the second octet – 168. Can we subtract 128 from 168? YES.

168-128 = 40
Next, can we subtract 64 from 40? NO. So, we assign a 0.

We move onto the next value. Can we deduct 32 from 40?. YES. We assign the value 1.

40 - 32 = 8
Next, can we subtract 18 from 8? NO. We assign 0.

Next, can we deduct 8 from 8? YES. We assign the value 1.

8-8 = 0
Since we have exhausted our decimal value, the will assign 0s to the remaining values in the table as shown.

Ultimately, the decimal 168 translates to the binary format 10101000. Again, if you sum up the decimal values corresponding to 1s in the bottom row you end up with 168. That is 128 + 32+8 = 168.
For the third octet, we have 1. The only number in our table that we can fully subtract from 1 is 1. So, we will assign the value 1 to 1 on the table and add preceding zeros as shown.

So the decimal value of 1 equates to the binary 00000001.
Lastly, we have 5. From the table, the only number that we can wholly subtract from 5 starts at 4. All the values to the left will be assigned 0.
Can we subtract 4 from 5? YES. We assign 1 to 4.

5-4 = 1
Next, can we subtract 1 from 2? NO. We assign the value 0.

Lastly, can we subtract 1 from 1? YES. We assign 1.

The decimal digit of 5 corresponds to the binary 00000101.
In the end, we have the following conversion.
192 => 11000000 168 => 10101000 1 => 00000001 5 => 00000101
So, 192.168.1.5 translates to 11000000.10101000.00000001.00000101 in binary form.
Understanding Subnet Mask / Network Mask
We have stated earlier that every host in a TCP/IP network should have a unique IP address, which in most cases is dynamically assigned by the router using the DHCP protocol. The DHCP protocol, (Dynamic Host Configuration Protocol) is a service that dynamically assigns an IP address to hosts in an IP network.
But how do you determine which part of the IP is reserved for the network section and which section is available for use by the host system? This is where a subnet mask or network mask comes in.
A subnet is an additional component to an IP address that distinguishes the network & host portion of your network. Just like an IP address, the subnet is a 32-bit address and can be written in either decimal or binary notation.
The purpose of a subnet is to draw a boundary between the network portion of an IP address and the host portion. For each bit of the IP address, the subnet or netmask assigns a value.
For the network portion, it turns on the bit and assigns the value of 1, For the host portion, it turns off the bit and assigns the value of 0. Therefore all bits set to 1 correspond to the bits in an IP address that represent the network portion whilst all bits set to 0 correspond to the bits of the IP that represent the host address.
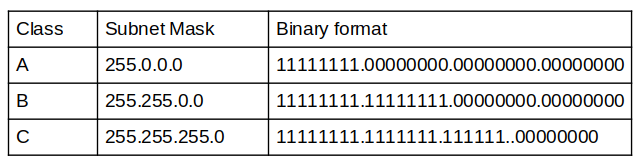
A commonly used subnet mask is the Class C subnet which is 255.255.255.0.
The table below shows the network masks in decimal and binary.
This wraps up part 2 of our networking essentials series. We have covered the decimal to binary IP conversion, subnet masks, and the default subnet masks for each class of IP address.